
Sadržaj:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:08.
- Zadnja izmjena 2025-01-23 14:37.



U ovom Instructable -u pokazat ću vam kako izgraditi igru Tic Tac Toe s AI -om pomoću Arduina. Možete igrati protiv Arduina ili gledati Arduino kako igra protiv sebe.
Koristim algoritam nazvan "minimaks algoritam", koji se može koristiti ne samo za izradu AI za Tic Tac Toe, već i za razne druge igre poput Four in a Row, dame ili čak šah. Igre poput šaha vrlo su složene i zahtijevaju mnogo profinjenije verzije algoritma. Za našu igru Tic Tac Toe možemo koristiti najjednostavniju verziju algoritma, koja je ipak prilično impresivna. U stvari, AI je toliko dobar da je nemoguće pobijediti Arduino!
Igra se lako gradi. Trebate samo nekoliko komponenti i skicu koju sam napisao. Dodao sam i detaljnije objašnjenje algoritma, ako želite razumjeti kako radi.
Korak 1: Izgradite i igrajte se
Za izradu igre Tic Tac Toe bit će vam potrebne sljedeće komponente:
- Arduino Uno
- 9 WS2812 RGB LED dioda
- 9 tastera
- nekoliko žica i kratkospojnih kabela
Spojite komponente kao što je prikazano na skici Fritzinga. Zatim prenesite kôd na svoj Arduino.
Prema zadanim postavkama, Arduino prvi skreće. Kako bi stvari bile zanimljivije, prvi potez odabire se nasumično. Nakon prvog poteza, Arduino koristi algoritam minimaksa kako bi odredio najbolji mogući potez. Počinjete novu igru resetiranjem Arduina.
Možete gledati kako Arduino "razmišlja" otvaranjem serijskog monitora. Za svaki mogući potez, algoritam izračunava ocjenu koja pokazuje hoće li ovaj potez dovesti do pobjede (vrijednost 10) ili gubitka (vrijednost -10) za Arduino ili remija (vrijednost 0).
Također možete gledati kako se Arduino igra sam protiv sebe tako što ćete na samom početku skice komentirati redak "#define DEMO_MODE". Ako učitate izmijenjenu skicu, Arduino nasumično pravi prvi potez, a zatim koristi minimaks algoritam za određivanje najboljeg poteza za svakog igrača u svakom potezu.
Imajte na umu da ne možete pobijediti protiv Arduina. Svaka utakmica će završiti neriješeno ili ćete izgubiti ako pogriješite. To je zato što algoritam uvijek bira najbolji mogući potez. Kao što možda znate, igra Tic Tac Toe uvijek će završiti neriješeno ako oba igrača ne pogriješe. U demo načinu rada svaka igra završava neriješeno jer, kao što svi znamo, računari nikada ne griješe;-)
Korak 2: Minimaksni algoritam

Algoritam se sastoji od dvije komponente: funkcije procjene i strategije pretraživanja. Funkcija vrednovanja je funkcija koja dodjeljuje numeričku vrijednost pozicijama ploče. Ako je pozicija konačna pozicija (tj. Pozicija na kojoj je plavi igrač ili crveni igrač pobijedio ili gdje nijedan igrač nije pobijedio), funkcija procjene je vrlo jednostavna: Recimo da Arduino igra plavo, a ljudski igrač crveno. Ako je pozicija dobitna pozicija za plavo, funkcija dodjeljuje vrijednosti 10 toj poziciji; ako je dobitna pozicija za crvenu boju, funkcija dodjeljuje vrijednost -10 poziciji; a ako je pozicija neriješena, funkcija dodjeljuje vrijednost 0.
Kad je red na Arduinu, želi izabrati potez koji maksimizira vrijednost funkcije procjene, jer maksimiziranje vrijednosti znači da će preferirati pobjedu nad remijem (10 je veće od 0) i omogućiti neriješeno nad gubitkom (0 je veće od -10). Analognim argumentom protivnica želi igrati na takav način da minimizira vrijednost funkcije procjene.
Za ne-konačnu poziciju, algoritam izračunava vrijednost funkcije evaluacije pomoću rekurzivne strategije pretraživanja. Polazeći od trenutne pozicije, naizmjenično simulira sve poteze koje plavi i crveni igrač mogu izvesti. Ovo se može vizualizirati kao stablo, kao na dijagramu. Kada dođe do konačne pozicije, počinje se odmaći noseći vrijednost funkcije procjene s nižeg nivoa rekurzije na viši nivo rekurzije. Ona dodjeljuje najveće (ako je u odgovarajućem koraku rekurzije na redu plavi igrač) ili minimalne (ako je u odgovarajućem koraku rekurzije na redu crveni igrač) vrijednosti funkcije evaluacije od donjeg nivoa rekurzije do pozicije na viši nivo rekurzije. Konačno, kada algoritam završi korak unatrag i ponovno stigne na trenutnu poziciju, bit će potreban taj potez (ili jedan od poteza) koji ima maksimalnu vrijednost funkcije procjene.
Ovo može zvučati pomalo apstraktno, ali zapravo nije tako teško. Uzmite u obzir položaj prikazan na vrhu dijagrama. U prvom koraku rekurzije postoje tri različita poteza koja plava može poduzeti. Plava pokušava maksimizirati vrijednost funkcije procjene. Za svaki od poteza koji plavi može poduzeti, postoje dva poteza koja crvena može napraviti. Crvena pokušava minimizirati vrijednost funkcije procjene. Razmislite o potezu gdje plava igra u gornjem desnom kutu. Ako crveni igra u centralnom polju, crveni je pobijedio (-10). Ako, s druge strane, crvena igra u središnjem donjem okviru, plava će pobijediti u sljedećem potezu (10). Dakle, ako se plava reproducira u gornjem desnom kutu, crvena će se igrati u središnjem okviru, jer to minimizira vrijednost funkcije procjene. Analogno, ako se plava reproducira u središnjem donjem okviru, crvena će se ponovno igrati u središnjem okviru jer to minimizira funkciju procjene. Ako, s druge strane, plava igra u središnjem okviru, nije važno koji potez crvena uzima, plava će uvijek pobijediti (10). Budući da plava želi maksimizirati funkciju ocjenjivanja, igrat će se u središnjem okviru, jer ta pozicija rezultira većom vrijednošću funkcije ocjenjivanja (10) od druga dva poteza (-10).
Korak 3: Rješavanje problema i daljnji koraci
Ako pritisnete dugme i zasvijetli drugačija LED lampica od one koja odgovara gumbu, vjerojatno ste pomiješali žice na pinovima A0-A2 ili 4-6 ili ste LED diode priključili pogrešnim redoslijedom.
Također imajte na umu da algoritam ne mora uvijek birati potez koji će omogućiti Arduinu da pobijedi što je brže moguće. U stvari, proveo sam neko vrijeme u otklanjanju grešaka u algoritmu jer Arduino nije odabrao potez koji bi bio dobitni potez. Trebalo mi je neko vrijeme dok nisam shvatio da je umjesto toga odabrao potez koji garantuje da će kasnije dobiti jedan potez. Ako želite, možete pokušati izmijeniti algoritam tako da uvijek preferira dobitni potez u odnosu na kasniji dobitak.
Moguće proširenje ovog projekta bilo bi korištenje algoritma za izradu AI za 4x4 ili čak 5x5 Tic Tac Toe. Međutim, imajte na umu da broj pozicija koje algoritam treba ispitati raste vrlo brzo. Morat ćete pronaći načine da učinite evaluacionu funkciju inteligentnijom dodjeljujući vrijednosti pozicijama koje nisu konačne, na osnovu vjerovatnoće da je pozicija dobra ili loša za dotičnog igrača. Također možete pokušati učiniti pretraživanje inteligentnijim tako što ćete prekinuti rekurziju ranije ako se pokaže da je potez manje vrijedan daljnjeg istraživanja od alternativnih poteza.
Arduino vjerojatno nije najbolja platforma za takva proširenja zbog svoje ograničene memorije. Rekurzija dozvoljava da stek raste tokom izvođenja programa, a ako se stek previše povećava, može oštetiti memoriju programa, što dovodi do rušenja ili nepravilnog ponašanja. Odabrao sam Arduino za ovaj projekt uglavnom zato što sam želio vidjeti može li se to učiniti i u obrazovne svrhe, a ne zato što je najbolji izbor za ovu vrstu problema.
Preporučuje se:
Python Tic Tac Toe igra: 4 koraka

Python Tic Tac Toe igra: python tic tac toe igra Ova igra je napravljena na pythonu koji je na računarskom jezikui koristio sam python editor pod nazivom: pycharm možete koristiti i normalni uređivač python koda
Arduino Touch Tic Tac Toe igra: 6 koraka (sa slikama)

Arduino Touch Tic Tac Toe igra: Dragi prijatelji, dobrodošli u još jedan Arduino vodič! U ovom detaljnom vodiču napravit ćemo igru Arduino Tic Tac Toe. Kao što vidite, koristimo ekran osjetljiv na dodir i igramo se protiv računara. Jednostavna igra poput Tic Tac Toe je
Elektronička igra igraonica "Tic-Tac-Toe" u drvenoj kutiji: 5 koraka

Elektronska igra Tic-Tac-Toe u drvenoj kutiji: Pozdrav Uvodim smiješnu igru Tic-Tac-Toe u novom izdanju. Pretražio sam sličan projekt na webu, ali ideja je ovdje jedinstvena.NADAM SE :) Pa krenimo sada
Tic Tac Toe: 12 koraka
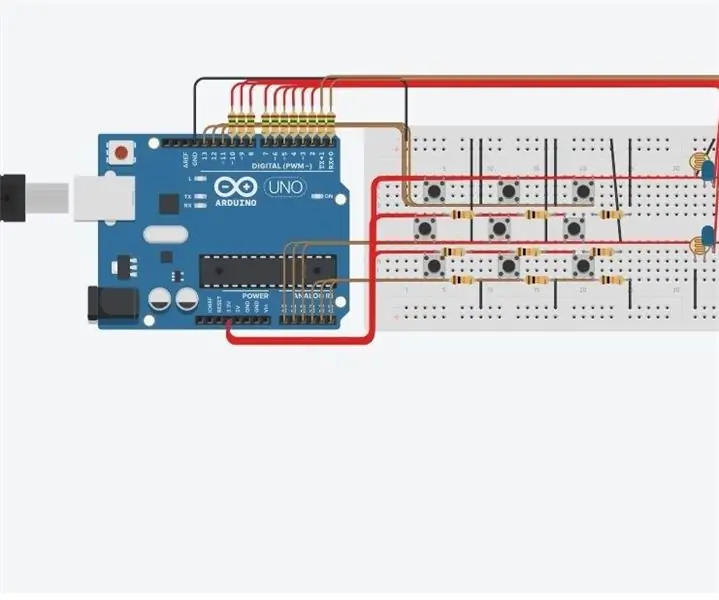
Tic Tac Toe: Danas ćemo raditi igru Tic Tac Toe na TinkerCad -u koristeći Arduino. Koristit ćemo mnogo jednostavnih komponenti i koristiti kôd da ih sve povežemo. Glavni dio ovog sklopa koji sve ovo spaja je kod. Ovaj napredak
Umjetna inteligencija za društvene igre: minimalni algoritam: 8 koraka
Umjetna inteligencija za društvene igre: Minimaksni algoritam: Jeste li se ikada zapitali kako nastaju računari protiv kojih igrate šah ili dame? Pa ne tražite dalje od ovog Instructable -a jer će vam pokazati kako napraviti jednostavnu, ali efikasnu umjetnu inteligenciju (AI) koristeći Minimax Algoritam! Korišćenjem
