Samobalansirajući robot pomoću PID algoritma (STM MC): 9 koraka

2024 Autor: John Day | [email protected]. Zadnja izmjena: 2024-01-30 08:08

U posljednje vrijeme puno je posla učinjeno na samobalansiranju objekata. Koncept samobalansiranja započeo je balansiranjem obrnutog klatna. Ovaj koncept se proširio i na dizajn aviona. U ovom projektu smo dizajnirali mali model samobalansirajućeg robota koristeći PID (proporcionalni, integralni, izvedeni) algoritam. Od tada je ova metoda novo lice sistema za upravljanje industrijskim procesima. Ovaj izvještaj daje pregled metoda uključenih u samobalansiranje objekata. Ovaj projekat je sproveden kao semestralni projekat radi razumijevanja korelacije PID -a o efikasnosti različitih industrijskih procesa. Ovdje se fokusiramo samo na kratak pregled efikasnosti i primjene PID kontrole. Ovaj dokument je napravljen kratkim uvodom u sisteme upravljanja i srodnu terminologiju, uz motivaciju za projekat. Eksperimenti i zapažanja su uzeti, zasluge i nedostaci su opisani i završavaju s budućim poboljšanjima. Model samobalansirajućeg robota razvijen je kako bi se razumjela efikasnost PID -a u svijetu upravljačkog sistema. Prolazeći kroz rigorozne testove i eksperimente, otkrivene su prednosti i nedostaci PID sistema upravljanja. Utvrđeno je da, uprkos mnogim prednostima PID kontrole u odnosu na prethodne metode, ipak ovaj sistem zahtijeva mnogo poboljšanja. Nadamo se da će čitalac dobro razumjeti važnost samobalansiranja, efikasnost i nedostatke PID kontrole

Korak 1: Uvod

Pojavom računara i industrijalizacijom procesa, kroz čitavu ljudsku istoriju, uvijek se istraživalo kako bi se razvili načini za rafiniranje procesa i, što je još važnije, za njihovo samostalno upravljanje pomoću mašina. Svrha je smanjiti čovjekovo uključivanje u ove procese, čime se smanjuje greška u tim procesima. Stoga je razvijeno polje „Inženjering upravljačkih sistema“. Inženjering upravljačkog sistema može se definirati kao korištenje različitih metoda za kontrolu rada procesa ili održavanje stalnog i preferiranog okruženja, bilo ručnog ili automatskog.

Jednostavan primjer može biti kontrola temperature u prostoriji. Ručna kontrola znači prisutnost osobe na lokaciji koja provjerava trenutne uvjete (senzor), uspoređuje je sa željenom vrijednošću (obrada) i poduzima odgovarajuće radnje da dobije željenu vrijednost (pokretač). Problem s ovom metodom je što nije pouzdana jer je osoba sklona greškama ili nemaru u svom poslu. Također, drugi problem je što brzina procesa koji pokreće pokretač nije uvijek ujednačena, što znači da se ponekad može dogoditi brže nego što je potrebno, a ponekad može biti sporo. Rješenje ovog problema bilo je korištenje mikrokontrolera za upravljanje sistemom. Mikrokontroler je

programirano za upravljanje procesom, prema zadanim specifikacijama, spojeno u kolo (o čemu će biti riječi kasnije), napaja željene vrijednosti ili uvjete i na taj način kontrolira proces radi održavanja željene vrijednosti. Prednost ovog procesa je što u tom procesu nije potrebna ljudska intervencija. Takođe, brzina procesa je ujednačena

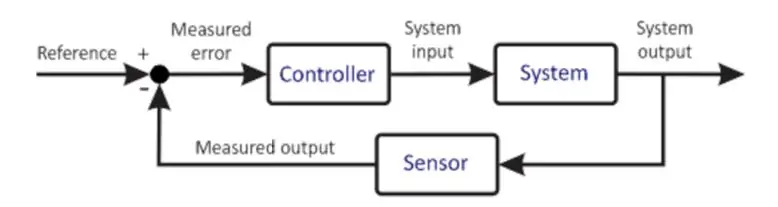
Osnovni sistem upravljanja

Prethodni dijagram prikazuje vrlo pojednostavljenu verziju upravljačkog sistema. Mikrokontroler je srce svakog kontrolnog sistema. To je vrlo važna komponenta, stoga njen odabir treba pažljivo obaviti na osnovu zahtjeva Sistema. Mikrokontroler prima ulaz od korisnika. Ovaj ulaz definira željeno stanje sistema. Mikrokontroler takođe prima povratnu informaciju od senzora. Ovaj senzor je spojen na izlaz Sistema, čije se informacije vraćaju na ulaz. Mikroprocesor, na osnovu svog programiranja, vrši različite proračune i daje izlaz aktuatoru. Pogon, na osnovu izlazne snage, kontroliše postrojenje kako bi pokušao da održi te uslove. Primjer bi mogao biti vozač motora koji upravlja motorom gdje je vozač pokretač, a motor pogon. Motor se, dakle, okreće zadanom brzinom. Priključeni senzor očitava stanje postrojenja u ovom trenutku i šalje ga nazad u mikrokontroler. Mikrokontroler ponovo uspoređuje, vrši proračune i tako se ciklus ponavlja. Ovaj proces se ponavlja i beskonačan je pri čemu mikrokontroler održava željene uslove

Korak 2: PID sistem upravljanja

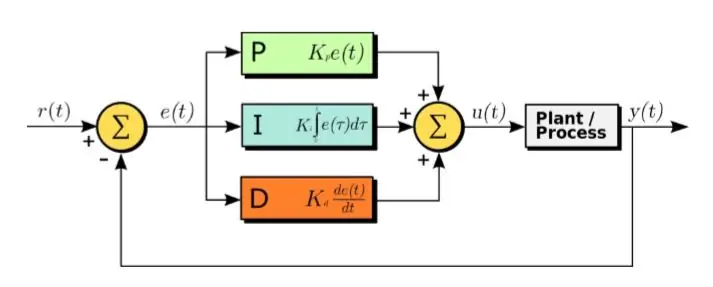
PID algoritam je efikasna metoda dizajniranja upravljačkog sistema.

Definicija

PID je kratica za Proporcionalno, Integralno i Derivativno. U ovom algoritmu primljeni signal greške je ulaz. I sljedeća jednadžba se primjenjuje na signal greške

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integral (e (t)) (1.1)

Kratko objašnjenje

Kao što se može vidjeti u gornjoj jednadžbi, integral i derivacija signala greške se izračunavaju, množe s odgovarajućim konstantama i dodaju zajedno s konstantom Kp pomnoženom s e (t). Izlaz se zatim dovodi do aktuatora koji pokreće sistem. Pogledajmo sada redom svaki dio funkcije. Ova funkcija direktno utječe na vrijeme porasta, vrijeme pada, vršno preko snimanja, vrijeme taloženja i grešku u stacionarnom stanju.

• Proporcionalni dio: proporcionalni dio smanjuje vrijeme porasta i smanjuje grešku u stacionarnom stanju. To znači da će sistemu trebati manje vremena da postigne svoju vršnu vrijednost, a kada dostigne stabilno stanje, greška u stabilnom stanju bit će mala. Međutim, povećava vršno prekoračenje.

• Derivativni dio: Derivativni dio smanjuje vrijeme prekoračenja i slijeganja. To znači da će prolazno stanje sistema biti više prigušeno. Takođe, sistem će za manje vremena postići stabilno stanje. Međutim, on nema utjecaja na vrijeme porasta ili grešku u stacionarnom stanju.

• Sastavni dio: Sastavni dio smanjuje vrijeme porasta i potpuno eliminira grešku u stacionarnom stanju. Međutim, povećava vršno prekoračenje i vrijeme taloženja.

• Podešavanje: Dobar kontrolni sistem imaće nisko vrijeme uspona, vrijeme slijeganja, vršno prekoračenje i grešku u stabilnom stanju. Stoga je potrebno Kp, Kd, Ki konačno prilagoditi kako bi se prilagodio doprinos gore navedenih faktora kako bi se stekao dobar sistem kontrole.

Slika je priložena i prikazuje učinak promjene različitih parametara u PID algoritmu.

Korak 3: Samo balansirajući robot

Samobalansirajući robot je višeslojni robot na dva kotača.

Robot će se pokušati uravnotežiti primjenom bilo koje nejednake sile. On će se uravnotežiti primjenom sile koja se suprotstavlja rezultantama sila na robotu.

Metode samo balansiranja

Postoje četiri metode samobalansiranja robota. Ovo su kako slijedi:

Samo balansiranje pomoću dva IC senzora nagiba

Ovo je jedan od najgrubljih načina za uravnoteženje robota jer zahtijeva vrlo malo hardvera i relativno jednostavan algoritam. U ovom pristupu, dva nagnuta IR senzora koriste se za mjerenje udaljenosti između tla i robota. Na osnovu izračunate udaljenosti, PID se može koristiti za pogon motora kako bi se u skladu s tim izbalansirao robot. Jedan nedostatak ove metode je to što IR senzor može propustiti neka očitanja. Drugi problem je što su prekid i petlje potrebni za izračunavanje udaljenosti što povećava vremensku složenost algoritma. Dakle, ovaj način balansiranja robota nije mnogo efikasan.

Samo balansiranje pomoću akcelerometra

Akcelerometar nam daje ubrzanje tijela u 3 osi. Ubrzanje orijentirano u osi y (prema gore) i osi x (prema naprijed) daje nam mjeru za izračunavanje smjera gravitacije i stoga izračunavanje kuta nagiba. Kut se izračunava na sljedeći način:

θ = arktan (Ay/Ax) (1.2)

Nedostatak korištenja ove metode je to što će se tijekom kretanja robota očitanjima dodati i horizontalno ubrzanje, što je visokofrekventna buka. Stoga će kut nagiba biti netočan.

Samo balansiranje pomoću žiroskopa

Za izračunavanje angluarskih brzina duž tri osi koristi se žiroskop. Kut nagiba dobiva se pomoću sljedeće jednadžbe.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

Jedan veliki nedostatak korištenja žiroskopa je to što ima mali DC Bias koji predstavlja niskofrekventni šum i za nekoliko vremena vraćene vrijednosti su potpuno pogrešne. Ovo će nakon integracije uzrokovati da se nulta točka udalji. Kao rezultat toga, robot će ostati u svom okomitom položaju neko vrijeme i prevrnut će se kada dođe do zanošenja.

Samo balansiranje pomoću akcelerometra i žiroskopa

Kao što je gore rečeno, korištenje samo akcelerometra ili žiroskopa neće nam dati pravi kut nagiba. Da bi se to objasnilo, koriste se i akcelerometar i žiroskop. Oba su ugrađena u MPU6050. Ovdje dobivamo podatke od oboje, a zatim ih spajamo ili pomoću Kalmanovog filtera ili komplementarnog filtera.

• Kalmanov filter: Kalmanov filter izračunava najbolju procjenu stanja dinamičkog sistema iz bučnih mjerenja, minimizirajući srednju kvadratnu grešku procjene. Radi u dvije faze, predviđanju i ispravljanju, s obzirom na diskretne stohastičke jednadžbe koje opisuju dinamiku sistema. Međutim, to je vrlo složen algoritam za implementaciju, posebno na ograničenom hardveru mikrokontrolera.

• Komplementarni filter: Ovaj algoritam prvenstveno koristi podatke dobijene od žiroskopa i integrira ih s vremenom da dobije kut nagiba. Također koristi mali dio očitanja akcelerometra. Komplementarni filter u stvari minimizira visokofrekventni šum akcelerometra i niskofrekventni šum žiroskopa, a zatim ih spaja kako bi dao najbolji tačan kut nagiba.

Korak 4: Dizajn robota

Dizajnirali smo samo balansirajućeg robota pomoću kontrolera proporcionalne izvedbe implementiranog pomoću komplementarnog filtera za MPU6050. Ovaj mali model samo balansirajućeg robota ilustrirat će nam korisnost upravljačkih sustava u samo balansirajućim robotima.

Implementacija sistema:

Sistem je samobalansirajući robot. Implementira se pomoću PID kontrolera koji je proporcionalni integralni derivativni kontroler. Uravnotežujemo robota vozeći njegove kotače u smjeru njegovog pada. Pritom pokušavamo zadržati težište robota iznad točke zakretanja. Da bismo pokrenuli kotače u smjeru njegovog pada, trebali bismo znati gdje robot pada i kojom brzinom pada. Do ovih podataka dolazi se pomoću MPU6050 koji ima akcelerometar i žiroskop. MPU6050 mjeri kut nagiba i daje svoj izlaz mikrokontroleru. MPU6050 je povezan sa STM pločom putem I2C. U I2C, jedna žica je za sat koji se naziva SCL. Drugi je za prijenos podataka koji je SDA. U ovom slučaju koristi se komunikacija master slave. Početna i završna adresa specificirane su tako da znaju odakle podaci počinju i gdje završavaju. Ovdje smo implementirali komplementarni filter za MPU6050 koji je matematički filter za spajanje izlaza akcelerometra i žiroskopa. Nakon što prikupi podatke iz MPU6050, mikrokontroler će izvršiti proračune kako bi znao gdje pada. Na osnovu proračuna, STM mikrokontroler će dati naredbe vozaču motora da vozi vozila u smjeru pada što će uravnotežiti robota.

Korak 5: Komponente projekta

Sljedeće komponente su korištene u projektu samobalansirajućeg robota:

STM32F407

Mikrokontroler dizajniran od strane ST Microelectronics. Radi na ARM Cortex-M arhitekturi.

Vozač motora L298N

Ova IC se koristi za pokretanje motora. Ima dva vanjska ulaza. Jedan iz mikrokontrolera koji mu šalje PWM signal. Podešavanjem širine impulsa može se podesiti brzina motora. Njegov drugi ulaz je izvor napona potreban za pogon motora, što je u našem slučaju baterija od 12V.

DC motor

DC motor radi na istosmjernom napajanju. U ovom eksperimentu, istosmjerni motor radi pomoću optokaplera spojenih na pogon motora. Za pogon motora koristili smo motorni pogon L298N.

MPU6050

MPU6050 se koristi za dobivanje informacija o tome gdje robot pada. Mjeri kut nagiba u odnosu na nultu točku nagiba koja je položaj MPU6050 kada program počne raditi.

MPU6050 ima troosni akcelerometar i troosni žiroskop. Akcelerometar mjeri ubrzanje duž tri osi, a žiroskop mjeri kutnu brzinu oko tri osi. Da bismo spojili izlaz, moramo filtrirati zvukove oba. Za filtriranje zvukova imamo Kalmanov i Dopunski filtar. U naš projekt smo implementirali komplementarni filter.

Opto par 4N35

Optokapler je uređaj koji se koristi za izolaciju niskonaponskog dijela i visokonaponskog dijela kola. Kako naziv govori, radi na bazi svjetlosti. Kad niskonaponski dio dobije signal, struja teče u visokonaponskom dijelu

Korak 6: Struktura robota

Struktura robota je objašnjena na sljedeći način:

Fizička struktura

Samobalansirajući robot sastoji se od dva sloja sastavljena od prozirnog plastičnog stakla. U nastavku su navedeni detalji dva sloja:

Prvi sloj

U donjem dijelu prvog sloja postavili smo ćeliju za napajanje STM ploče. Takođe su sa svake strane postavljena dva motora od po 4 volta sa povezanim gumama za kretanje robota. U gornji dio prvog sloja postavljene su dvije baterije od po 4 volta (ukupno 8 volti) i upravljački sklop motora (L298N) za rad motora.

Drugi sloj

U gornjem sloju robota postavili smo STM ploču na Perf Board. Još jedna perf ploča sa 4 opto spojnice postavljena je na gornji sloj. Žiroskop se također postavlja na gornji sloj robota s donje strane. Obje komponente smještene su u srednji dio tako da se težište drži što je moguće niže.

Centar gravitacije robota

Težište se održava što je moguće niže. U tu smo svrhu na donji sloj postavili teške baterije, a na gornji sloj lagane komponente, poput STM ploče i optokaplera.

Korak 7: Kodirajte

Kod je sastavljen na Atollic TrueStudio. STM studio je korišten za otklanjanje grešaka.

Korak 8: Zaključak

Nakon mnogo eksperimentiranja i promatranja, konačno dolazimo do tačke u kojoj sumiramo naše rezultate i raspravljamo o tome koliko smo uspjeli implementirati i razraditi efikasnost sistema.

Opšti pregled

Tijekom eksperimentiranja, brzina motora uspješno je kontrolirana pomoću PID algoritma. Krivulja ipak nije baš glatka ravna linija. Za to postoji mnogo razloga:

• Senzor iako je spojen na niskopropusni filter i dalje pruža određene konačne prekide; to je zbog nelinearnih otpora i nekih neizbježnih razloga analogne elektronike.

• Motor se ne okreće glatko pod malim naponom ili PWM. Pruža trzaje koji mogu uzrokovati neke pogrešne vrijednosti unesene u sistem.

• Zbog ljuljanja, senzor može propustiti neke proreze koji pružaju veće vrijednosti. • Drugi glavni razlog grešaka može biti frekvencija takta jezgre STM mikrokontrolera. Ovaj model STM mikrokontrolera daje jezgru takta 168MHz. Iako se u ovom projektu bavio ovim problemom, postoji općenito mišljenje o ovom modelu da ne pruža baš tako visoku frekvenciju.

Brzina otvorene petlje pruža vrlo glatku liniju sa samo nekoliko neočekivanih vrijednosti. PID algoritam također radi u redu pružajući vrlo kratko vrijeme taloženja motora. PID algoritam motora testiran je pod različitim naponima održavajući referentnu brzinu konstantnom. Promjena napona ne mijenja brzinu motora i pokazuje da PID algoritam radi ispravno

Efikasnost

Ovdje raspravljamo o učinkovitosti PID kontrolera koju smo uočili tijekom eksperimentiranja.

Jednostavna implementacija

U odjeljku eksperimentiranja i zapažanja vidjeli smo da je PID kontroler vrlo jednostavan za implementaciju. Potrebna su samo tri parametra ili konstante koje je potrebno postaviti kako bi se imao sistem kontrole brzine

Nenadmašna efikasnost za linearne sisteme

Linearni PID kontroler je najefikasniji u porodici kontrolera jer je logika vrlo jednostavna i primjena je široko rasprostranjena u slučaju linearnih ili prilično linearnih aplikacija.

Ograničenja

Apstraktno smo objasnili ograničenja ovog sistema. Ovdje raspravljamo o nekoliko njih koje smo primijetili.

Izbor konstanti

Vidjeli smo da, iako je PID kontroler jednostavan za implementaciju, ipak je veliki nedostatak sistema što je korak odabira vrijednosti konstanti naporan; jer se moraju napraviti teški proračuni. Drugi način je hit i trial metoda, ali ni ona nije efikasna.

Konstante nisu uvijek konstantne

Eksperimentalni rezultati su pokazali da je za različite vrijednosti referentne brzine motora PID regulator neispravan za iste vrijednosti PID konstanti. Za različite brzine, konstante su se morale birati različito i to eksponencijalno povećava računske troškove.

Nelinearno

PID kontroler koji se koristi u našem slučaju je linearan, stoga se može primijeniti samo na linearne sisteme. Za nelinearne sisteme, kontroler se mora implementirati različito. Iako su dostupne različite nelinearne metode PID -a, one zahtijevaju odabir više parametara. Ovo opet čini sistem nepoželjnim zbog visokih troškova izračunavanja.

Potreban početni pritisak

U odjeljku eksperimentiranja pokazali smo da je za prilično malu referentnu brzinu gdje je greška prilično mala u startu, PWM koji isporučuje PID toliko mali da ne generira potrebni zakretni moment za motor. Dakle, motor u nekim ispitivanjima ne radi ili u drugim pokušajima omogućuje veliko prekoračenje i duže vrijeme taloženja.

Korak 9: Posebno hvala

Posebno hvala članovima moje grupe koji su mi pomogli u ovom projektu.

Uskoro ću postaviti link do videa.

Nadam se da će vam ovo uputstvo biti zanimljivo.

Ovo je Tahir Ul Haq iz UET -a koji se odjavljuje. Živjeli !!!