Sadržaj:
- Korak 1: Importer Librerías
- Korak 2: Evalúa La Función
- Korak 3: Asigna varijable De Las Coordenadas
- Korak 4: Konstrukcija Del Trapecio Según Coordenadas Y Función
- Korak 5: Calcular El Área Del Trapecio Dentro De La Función
- Korak 6: Gráfica En Pyplot
- Korak 7: Organización De La Gráfica
- Korak 8: ¡Lo Lograste
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:06.
- Zadnja izmjena 2025-01-23 14:37.
Antes que nada, para desarrollar este program debes instalar la plataforma Python desde su página oficial:. Možda je preporučljivo instalirati verziju 2.7.12 od 64 bita.
Korak 1: Importer Librerías

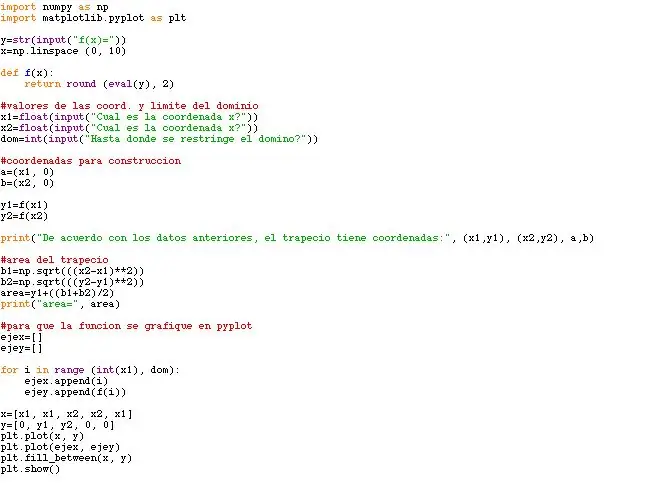
Este programi zahtijevaju slobodne dentro programe: matplotlib.pyplot y pylab. En la foto adjunta e este paso se puede ver que haciendo uso de los comandos from, import y as el programa puede accender a la información de las dos librerías usadas por este programa.
iz pylab uvoza
uvozite matplotlib.pyplot kao plt
VAŽNO: ¡POR FAVOR NO PONGAS TILDES EN NINGUNA PALABRA NI NINGÚN SÍMBOLO DEL ESPAÑOL! DE LO CONTRARIO SE CERRARÁ EL PROGRAMA Y NO SE GUARDARÁN LOS CAMBIOS QUE HICISTE
Korak 2: Evalúa La Función

Hay ciertas cosas que no puedes calcular sin saber ciertos datos que el program no te puede dar, a menos que le preguntes al usuario (es decir el que va a utilizar el program después de su creación) los valores de ciertas varijable; en este caso debemos preguntarle al usuario por la función a la cual le quieras calcular el área.
Ako ste već koristili al tipo de función, debes hacer uso de los comandos stream (str) i input. stream es un comando que permite uvodne varijable algebarske (como "x" y "y") dentro de un conjunto numérico y que se entiendan como números desconocidos dentro de la ecuación, es decir que permite calcular, por ejemplo, x^2+5 y que entienda a "x" como un número que no se conoce. Por otro lado, input permite que el valor que unozcas kuando el program pregunte por la variable sea el que adquiera por el resta del programa. La función linspace sirve para restringir los valores del eje a los indicados dentro del paréntesis.
En este caso, se necesita definir la la "y" por medio de una función
y = str (ulaz ("f (x) ="))
x = np.linspace (0, 10) def f (x): povratna runda (eval (y), 2)
Korak 3: Asigna varijable De Las Coordenadas

Para que las coordenadas cartesianas se puedan graficar, es necesario que el program pregunte al usuario los valores que toma la función en el eje x. Dado que estos son valores valores enteros, se debe volver a usar input, que permite que el valor que unozcas cuando el programa pregunte por la variable sea el que adquiera por el resta del programa. Para que el programa pregunte las varijable cuando lo pongas funkcionar, debes usar print para que la pregunta aparezca en la ventana SHELL. En este caso, se necesita sabre los dos valores de x y la limitedción del dominio.
Recuerda que el dominio son los valores del eje x en una función.
#valores de las coord. y limite del dominiox1 = float (input ("Cual es la coordenada x?")) x2 = float (input ("Cual es la coordenada x?")) dom = int (input ("Hasta donde se restringe el domino?")))
Korak 4: Konstrukcija Del Trapecio Según Coordenadas Y Función

Para construir el polígono, ya se tienen los valores que adquiere la función en x. Ahora, para los valores de y y (x1, 0) y (x2, 0), prikazuje asigna con las varijable y = f (x) y otro nombre para las previamente mencionadas.
#coordenadas para construcciona = (x1, 0) b = (x2, 0) y1 = f (x1) y2 = f (x2)
print ("De acuerdo con los datos anteriores, el trapecio tiene coordenadas:", (x1, y1), (x2, y2), a, b)
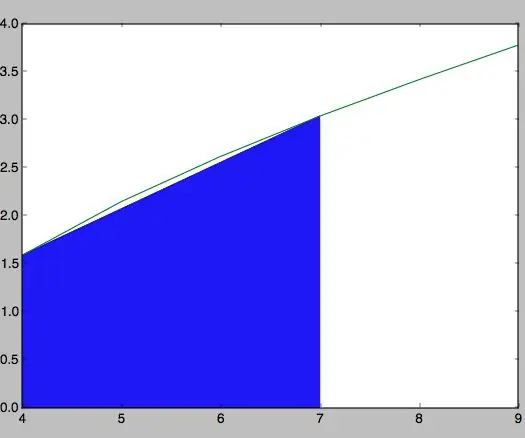
Korak 5: Calcular El Área Del Trapecio Dentro De La Función
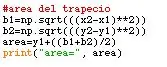
Para este paso, de de tener en cuenta la forma del trapecio, es decir, que tiene dos bases y la altura. Las baze i este caso mogu se pronaći u medio de la raíz cuadrada de la resta de los valores de x1 y x2 al cuadrado. Lo mismo ocurre para los valores de y1 y y2.
Para hallar el área total, es la suma de la altura y las bases sobre dos.
#area del trapeciob1 = np.sqrt (((x2-x1) ** 2)) b2 = np.sqrt (((y2-y1) ** 2)) area = y1+((b1+b2)/2) ispis ("area =", područje)
Korak 6: Gráfica En Pyplot

#para que la funcion se grafički prikazuje na piplotu
ejex =
ejey =
za i u rasponu (int (x1), dom):
ejex.append (i) ejey.append (f (i))
Para que la función se grafique hay que asignar los ejes x & y, pero como ya hay muchas varijable con esos nombres, asigna unos que identifiques como los ejes y no otras varijable. Dodatni uvjeti za organizaciju i in range su funkcionalnost de acuerdo con los parámetros establecidos al inicio del programa.
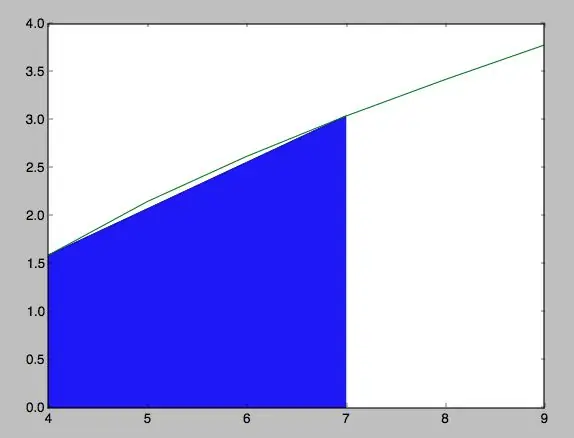
Korak 7: Organización De La Gráfica

x = [x1, x1, x2, x2, x1] y = [0, y1, y2, 0, 0]
plt.plot (x, y)
plt.plot (ejex, ejey) plt.fill_between (x, y) plt.show ()
En este paso se organizan las coordenadas de manera que koincidenta con la gráfica en sus respectivos ejes. Por otro lado, es donde se rellena el espacio del trapecio en donde se va a Calcular el área y se muestra la gráfica.
Korak 8: ¡Lo Lograste
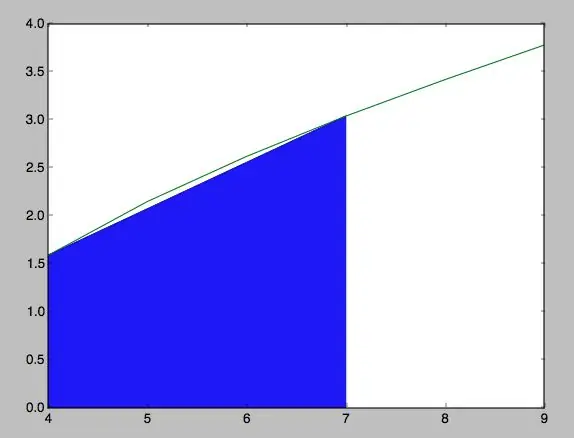

Después de haber seguido todos los pasos, encontrarás que tu program debe ser muy similar a lo que hay en las fotos adjuntas. Obviamente, los valores de las coordenadas y la función varían según como tú quieras ponerlos, y por ende, el área y la forma de la la curva.
Preporučuje se:
Como Crear Un Programs En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: 5 koraka
Como Crear Un Programs En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: Ovaj tutorijal se nalazi ñ ara i proračunata el površina koja je zakrivljena sa datotekama koje su važne za arhiviranje. Para ello se izračunava el area upotreba muchos trapecios sumados y se colorear á el area bajo esta
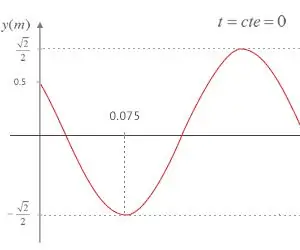
Como Hallar El Recorrido De Un Objeto Y El Área Bajo La Curva En Python: 7 koraka

Como Hallar El Recorrido De Un Objeto Y El Área Bajo La Curva En Python: Este programi gr á fica la curva que existe entre la relaci ó n velocidad contra tiempo en el movimiento de un object. Adem á s este program Calcula el recorrido que hizo este Objeto al encontrar el á rea debajo de la curva que
Área Bajo La Curva: 7 koraka
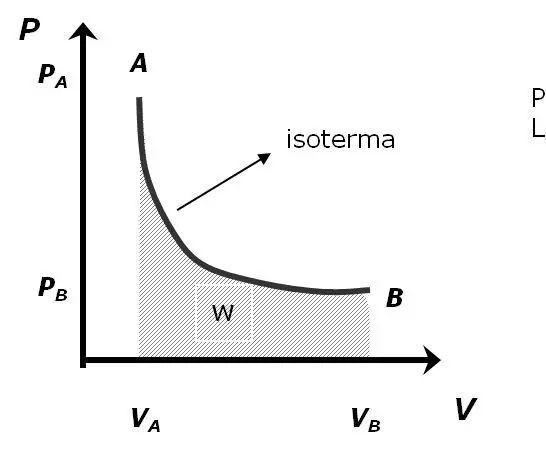
Área Bajo La Curva: Es necesario hallar el á rea bajo la curva de una funci ó n presi ó n contra volumen para poder hallar el trabajo (W) que de esta, teniendo en cuenta los principios de la f í sica Para hacer el trabajo m á s f á cil a
Desplazamiento De Un Objeto Mediante El Calculo De Área En Python: 8 koraka (sa slikama)
Desplazamiento De Un Objeto Mediante El Calculo De Área En Python: Para kalkulatorno el desplazamiento de un objeto, teniendo en cuenta los principios de la f í sica, moguće je postaviti en á rea de su movimiento en una gr á fica de vempo . Sin embargo, kalkulacija imovine
Como Crear Un Program za Python Que Grafique Cualquier Funkcija Y Saque Un Área Especifica Debajo De Ella: 6 koraka

Como Crear Un Program De Python Que Grafique Cualquier Funkcija Y Saque Un Área Especifica Debajo De Ella: Este program permite al usuario uvodio kualquier funci ó n, graficarla y deterar un un area especifica debajo de la misma
